Math is a subject that has many theories and number sets that are fascinating to learn about. One such fascinating number sets are prime numbers. Whether you are just starting to explore this concept or looking to sharpen your understanding, this article will guide you through the basics and beyond.
We will cover what prime numbers are, look at a prime number chart, explore examples, and even tackle some practice problems together. Let us get started!
Generated image
Defining Prime Numbers
A prime number is a whole number that is greater than 1 and is divisible by only 1 and itself without leaving a remainder. In other words, if you try to divide a prime number by any other whole number, it will not work out evenly.
For instance, consider the number 5. If you divide 5 by any number except for 1 and 5, you will always have a remainder other than ‘0’. By this, we can conclude that ‘5’ is a prime number. On the other hand, the number 4 can be divided evenly by 1, 2, and 4, leaving the remainder ‘0’ which does not follow the conditions to be a prime number.
Importance of Prime Numbers
You might wonder why we care so much about these special numbers. Prime numbers are the building blocks of the number system. They play a crucial role in various fields such as cryptography, computer algorithms, and number theory. Much of modern encryption relies on the properties of prime numbers to secure data.
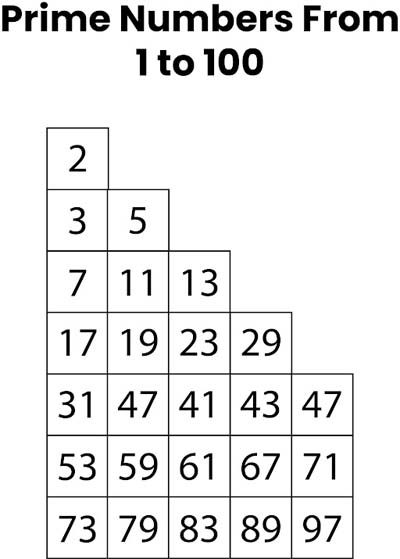
Prime Number Chart
To give you a visual idea of what prime numbers look like, here is a chart of the prime numbers between 1 and 100:
Prime Numbers (1-100)
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
By looking at this chart, you can see which numbers in this range are prime. if you notice, 2 is the only even prime number among all the even numbers that we know. This is because every other even number can be divided by 2, concluding that they are not prime.
Examples of Prime Numbers
To better understand prime numbers, let us go through a few more examples:
Example 1: The number 11
Divisors: 1 and 11
Since 11 is not divisible by any other number, it is a prime number.
Example 2: The number 15
Divisors: 1, 3, 5, and 15
Since 15 is divisible by the numbers 3 and 5 in addition to the numbers 1 and 15, it is not a prime number.
Example 3: The number 23
Divisors: 1 and 23
Since 23 is not divisible by any other number, we can conclude that it is a prime number.
Practice Problems
Now that we have covered the basics, let us put the knowledge to the test with some practice problems. Grab a pen and paper, and see if you can determine whether the following numbers are prime:
Is 29 a prime number?
Is 42 a prime number?
Is 53 a prime number?
Is 60 a prime number?
Is 97 a prime number?
Answers –
- ‘29’
- ‘42’
- ‘53’
- ‘60’
- ‘97’
Divisors: 1 and 29
Answer: Yes, 29 is a prime number.
Divisors: 1, 2, 3, 6, 7, 14, 21, 42
Answer: No, 42 is not a prime number.
Divisors: 1 and 53
Answer: Yes, 53 is a prime number.
Divisors: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Answer: No, 60 is not a prime number.
Divisors: 1 and 97
Answer: Yes, 97 is a prime number.
Fun Facts About Prime Numbers
Here are some fun facts that will make you more curious about prime numbers:
Twin Primes: These are sets of prime numbers that have a difference of 2. Examples include (3, 5), (11, 13), and (17, 19). Mathematicians are still researching whether there are infinitely many twin primes.
Mersenne Primes: These are prime numbers that can be written in the form 2^p – 1, where p is also a prime number. For example, 31 is a Mersenne prime because it can be written as 2^5 – 1.
Largest Known Prime: As of now, the largest known prime number is 2^82,589,933 – 1, a number with over 24 million digits! This was discovered in December 2018.
How to Find Prime Numbers
Finding prime numbers can be done using various methods, but one of the most common techniques is the Sieve of Eratosthenes. Here is a simple way to do it:
- Write down all the numbers from 2 up to your desired limit.
- Start with the first number (2). Circle it, as it is a prime number.
- Cross out all multiples of 2.
- Move to the next uncrossed number (3). Circle it.
- Cross out all multiples of 3.
- Continue this process until you have circled all the prime numbers in your range.
This method efficiently filters out non-prime numbers, leaving you with only the primes.
Conclusion
Prime numbers may seem simple at first glance, but they hold a world of complexity and importance in mathematics and beyond. From their basic definition to their applications in modern technology, prime numbers are truly remarkable. Remember, they are the building blocks of the number system, and understanding them is key to unlocking more advanced mathematical concepts.
So next time you encounter a prime number, take a moment to appreciate its unique properties and the role it plays in the vast universe of numbers.
Happy learning, and keep exploring the wonders of math!
For more such informative/interesting blogs, visit Center Point School.